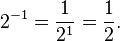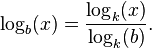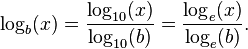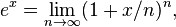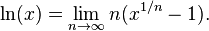تصاوير جشن قبولي هاي در مدارس تيزهوشان و نمونه دولتي در شهرهاي مختلف را اينجا ببينيد...

عکس هاي جشن شهرهاي ديگر نيز به زودي در همين قسمت قرار خواهد گرفت.
اگر می خواهد عکس های جشن قبولی بقیه ی شهر ها را ببینید به ادامه ی مطلب بروید.

چهارمین المپیاد ریاضی نوجوانان ایران برگزار می شود: مرحله ی اول : دوم اسفندماه 1392 مرحله ی دوم:پنجم اردیبهشت ماه 1393 مهلت ثبت نام: بیستم دی ماه 1392 |
ثبت نام چهارمین دوره
نحوه برگزاری چهارمین دوره المپیاد ریاضی نوجوانان ایران در سال تحصیلی 93-1392 به شرح زیر است:
1) شرکت کنندگان
این المپیاد در پایه های ششم ابتدایی، هفتم (اول متوسطه 1)، سوم راهنمایی و اول دبیرستان برگزار می شود. در هر سال تحصیلی به تفکیک پایه آزمون طراحی می شود و هر نفر با دانش آموزان هم پایه خود رقابت خواهد کرد.
2) شرط ورود به آزمون
شرط ورود به آزمون کلیه دانشآموزان ممتاز در درس ریاضی اجازه شرکت در آزمون را خواهند داشت. برای شرکت
در این المپیاد تکمیل فرم ثبتنام، ارایه یک عکس و پرداخت هزینه ثبتنام که مبلغ 80000 ریال ضروری است.
تبصره 1: مدارسی که به تعداد داوطلبان خود کتاب پرسشهای نخستین ، دومین و یا سومین المپیاد را خریداری کنند از تخفیف %40 قیمت پشت جلد کتاب بهرهمند خواهند شد.
تبصره 2: پذیرفتهشدگان مرحله اول برای شرکت در آزمون مرحله دوم نیز مبلغ 80000 ریال پرداخت خواهند کرد.
3) مراحل المپیاد
این المپیاد در دو مرحله و بهصورت هماهنگ کشوری برگزار میشود. مرحله اول این المپیاد در دوم اسفندماه 92 در سراسر کشور اجرا میشود. برگزیدگان این مرحله برای شرکت در مرحله دوم که در پنجم اردیبشهت ماه 93 برگزار میگردد، دعوت میشوند.
4) شرایط ورود به مرحله دوم
کسانی که بیش از %50 نمره را کسب کنند یا رتبه آنها کمتر از %5 شرکت کنندگان آن پایه باشد، به مرحله دوم صعود خواهند کرد. مرحله دوم آزمون نیز مشابه آزمون مرحله اول ، ولی شامل 30 پرسش می باشد.
تبصره: در صورتیکه مرکز آموزشی در هر پایه بیش از 10 نفر شرکت کننده داشته باشد و هیچ کدام از نفرات امتیاز لازم جهت ورود به مرحله دوم را نداشته باشد- جهت ایجاد امکان مضاعف برای دانش آموزان آن مرکز رتبه اول دانش آموزان هر پایه آن ها به مرحله دوم راه خواهد یافت.
5) پرسشهای آزمون
پرسشهای آزمون در هر دو مرحله به صورت 5 گزینهای خواهد بود. مرحله اول آزمون شامل 24 پرسش است. 10 پرسش آزمون 3 نمرهای، 8 پرسش آزمون 4 نمرهای و 6 پرسش آزمون 5 نمرهای است. به این ترتیب آزمون مرحله اول 92 نمره خواهد داشت. پرسشهای سطح اول نمره منفی ندارند، ولی برای پاسخهای نادرست پرسشهای سطح 2، یک نمره منفی و سطح 3، دو نمره منفی منظور خواهد شد.
تبصره1: در مرحله اول تعدادی از پرسش ها؛ از پرسش های المپیادهای سه دوره گذشته و یا مشابه آن ها انتخاب خواهد شد.
تبصره 2: تعدادی از پرسش ها با توجه به محتوای کتاب های ریاضی پایه مربوطه؛ طراحی خواهد شد.
6) برگزیدگان المپیاد و جوایز آن ها
الف) نفرات اول تا پنجم کشوری در هر پایه تندیس، مدال، لوح تقدی و جایزه ی نفیس (میزان مبلغ جایزه متعاقبا اعلام می گردد)
ب) نفرات اول هر استان در هر پایه به شرط کسب مدال و حداقل 40 درصد نمره مرحله دوم، مدال، تندیس، لوح تقدیر و با توجه به رنگ مدال جوایزی نفیس (میزان مبلغ جایزه متعاقبا اعلام می گردد)
ج) 10 نفراول هر پایه تحصیلی(رتبه 1 تا 10)مدال طلاو لوح تقدیر،20 نفر دوم(رتبه 11 تا30) مدال نقره و لوح تقدیر، 30 نفر سوم( رتبه 31 تا60) مدال برنز دریافت و لوح تقدیر دریافت خواهند کرد.
تبصره: رتبه های مساوی به تعداد تکرار شده، شمارش خواهند شد.
در ضمن کلیه مدال آوران جوایزی از محصولات انتشارات مبتکران را دریافت خواهند کرد.
• انتشارات مبتکران به پاس توجه و پیگیری امور مربوط به المپیاد ریاضی نوجوانان ایران به 3 نفر از مدیران مدارس شرکت کننده (تهران و شهرستان) که بیشترین مدال آوران المپیاد را دارا باشند، جوایزی اهدا خواهد کرد.
• از اولیا دانش آموزان ممتازی که فرزندان آن ها در 2 سال متوالی بهترین رتبه را نسبت به سایر دانش آموزان کسب کرده اند نیز با اهدا جوایزی تقدیر به عمل خواهد آمد.
لازم به ذکر است خانواده های برتری که در اختتامیه دومین دوره المپیاد مورد تقدیر قرار گرفتند، شامل این امتیاز نخواهند شد.
• جوایز این افراد در پایان سال تحصیلی و در جشن پایانی " المپیاد ریاضی نوجوانان ایران" که توسط موسسه فرهنگی آموزشی انتشاراتی مبتکران برگزار خواهد شد، اهدا می گردد.
7) مهلت ثبت نام
مهلت ثبتنام در دفاتر نمایندگیهای مبتکران در سراسر کشور تا پایان بهمن 92 است.
برای کسب اطلاعات بیشتر با شماره تلفن های زیر تماس بگیرید:
دبیرخانه المپیاد ریاضی نوجوانان ایران 61094201-021 الی 2
ثبت نام مدارس در استان ها: دفاتر نمایندگی مبتکران در سراسر کشور
ثبت نام مدارس تهران: 61094309-021
داوطلبان انفرادی: 61094101-021 الی 2
مدارس برای دسترسی بهلینک پیش ثبت نام کلیک کنید.
منبع: دبیرخانه المپیاد ریاضی نوجوانان ایران
برای پیش ثبت نام در چهارمین المپیاد ریاضی نوجوانان ایران به سایت مبتکران بروید به نشانی www.mobtakeran.com و فرم چهارمین المپیاد ریاضی نوجوانان را تکمیل کنید
نتایج آزمون ورودی مدارس استعدادهای درخشان این استان روز هشتم خرداد ماه اعلام می شود.
به گزارش روابط عمومی آموزش و پرورش خراسان رضوی ، جلال صداقت افزود: آزمون ورودی مدارس استعدادهای درخشان و نمونه دولتی در این استان همزمان با سراسر کشور روزهای 19 و 20 اردیبهشت ماه برگزار شده بود.
وی اظهارداشت: دانش آموزان شرکت کننده در آزمون مزبور می توانند در تاریخ اعلام شده با اطلاعات ثبت نامی خود به سایت اداره کل آموزش و پرورش خراسان رضوی مراجعه و نتیجه آزمون خود را دریافت نمایند.
وی گفت: امسال برای ورود به مدارس استعدادهای درخشان و نمونه دولتی این استان در مقطع متوسطه 28 هزار و 377 نفر و در مقطع راهنمایی 37 هزار و 531 نفر در آزمون ورودی این مدارس شرکت کردند.
صداقت اظهارداشت: پذیرش دانش آموزان برای ورود به مدارس نمونه دولتی بر اساس نمره آزمون ورودی و معدل کل آنان خواهد بود.
وی با بیان اینکه در آزمون ورودی مقطع راهنمایی معدل کل پایه پنجم و در آزمون ورودی متوسطه معدل کل پایه دوم راهنمایی ملاک خواهد بود، گفت:80 درصد نمره آزمون و 20 درصد معدل کل دانش آموز در قبولی آنان تاثیر دارد.
وی افزود: گزینش دانش آموزان برای ورود به مدارس استعدادهای درخشان صرفا بر اساس رتبه فضلی مبتنی بر نمره تراز شده آزمون خواهد بود.
وی اظهار داشت: در تعیین رتبه فضلی هر داوطلب نمره تراز شده آزمون فقط با دیگر داوطلبان متقاضی مدارس انتخابی وی به ترتیب اولویت سنجیده می شود.
صداقت گفت: حدود هفت هزار نفر در دبیرستانهای نمونه دولتی و استعدادهای درخشان و حدود پنج هزار نفر در مدارس راهنمایی نمونه دولتی و استعدادهای درخشان این استان پذیرفته می شوند.
برای ورودبه سایت آموزش وپرورش استان خراسان رضوی
روی تصویرزیرکلیک کنید.
برخی فرمولهای مورداستفاده درحل سوالات آزمونهای ورودی مدارس خاص
ازکتاب جامع تیزهوشان
درادامه مطلب
برخی فرمولهایی که درحل مسائل ریاضی به ماکمک می کنند
1-مجموع زواياي داخلي يك چند ضلعي از روش زير استفاده مي كنيم: براي پيدا كردن
180×(2-تعداد اضلاع)
مثال:مجموع زاويه هاي شكل مقابل چند درجه است؟
جواب: 1080=180×(2-8)
بقیه در ادامه ی مطلب بروید
هرگاه چند نقطهی متمایز(جدا از هم)،بر روی یک خط راست باشند تعداد پاره خط ها از فرمول زیر به دست می آید.
2 ÷ (تعداد فاصله ها × تعداد نقطه ها ) = تعداد پاره خط ها
توجه : تعداد فاصلهها همیشه یکی کمتر از تعداد نقطهها است.
2-هرگاه چند نقطهی متمایز،بر روی خط راست باشند، تعداد نیم خطها از فرمول زیر،به دست می آید.
2 × تعداد نقطهها = تعداد نیم خطها
3-هرگاه چند نقطهی متمایز، برروی یک نیم خط باشند،تعداد نیم خطها مانند مثال زیر به دست میآید.
مثال: برروی یک نیم خط،هفت نقطهی متمایز وجود دارد چند نیم خط،در شکل وجود دارد؟
پس (8 = 1 + 7 ) نقطه داریم یعنی 8 نیم خط خواهیم داشت.
4- هرگاه چند نقطهی متمایز، برروی یک پاره خط باشند نیم خطی، درشکل وجود ندارد.
برش و قسمت:
وقتی می خواهیم یک قطعه یا جسمی رشته مانند را به قسمت های مساوی ویا نامساوی تقسیم کنیم همیشه تعداد قسمتها یکی بیشتر از تعداد برشها است.
مثال: یک آهنگر , میله ای به طول 12 متر را به چهار قسمت تقسیم کرد او برای این کار چند برش زده است؟
برش 3 = 1 – 4 (قسمت)
مجموع و اختلاف:
هرگاه مجموع دو عدد و اختلاف آن دو عدد را به ما بدهند و آن دو عدد را از ما بخواهند، از دو راه زیر به دست میآید.
1-اگر مجموع واختلاف را از هم کم کرده،بر2 تقسیم کنیم عدد کوچکتر به دست میآید.
2- اگر مجموع واختلاف را با هم جمع کرده،بر2 تقسیم کنیم عدد بزرگتربه دست میآید.
تعداد یک رقم در یک مجموعهی اعداد متوالی
1-از عدد1 تا 99 از همهی رقمها 20 تا داریم به جز رقم(صفر)،که از آن 9 تا داریم.
2-از عدد 100تا 199 از همهی رقمها 20تا داریم به جز رقم(یک)،که از آن 120 تا داریم.
3- از عدد 200تا 299 از همهی رقمها 20تا داریم به جز رقم(دو)،که از آن 120 تا داریم و ...
تعداد اعداد
در مجموعه اعداد طبیعی (از یک شروع میشود)تعداد اعداد یک رقمی9 تا،اعداد دو رقمی 90تا،اعداد سه رقمی 900تا،اعداد چهاررقمی 9000 تاو... می باشد.
تعیین تعداد عددهای صحیح یک مجموعهی اعداد متوالی
1-اگر تعداداعداد،از عدد اولی تا عدد آخری مورد نظر باشد از فرمول زیر،استفاده میشود.
1 + (عدد اولی – عدد آخری) = تعداد اعداد
مثال: از عدد27 تا عدد 1027 چند عدد صحیح (عددی که کسری و اعشاری نباشد) وجود دارد؟
تعداد اعداد 1001 = 1+(27 – 1027 )
2-اگر تعداد اعداد،بین دو عدد اولی و آخری مورد نظر باشد از فرمول زیر،استفاده میشود.
1 – ( عدد اولی – عدد آخری) = تعداد اعداد
3- اگر تعداد اعداد زوج و یا فرد یک مجموعهی اعداد متوالی مورد نظر باشد از فرمولهای زیر استفاده میشود.
1+ 2÷(کوچکترین عدد زوج – بزرگترین عدد زوج) = تعداد اعداد زوج
1 + 2÷(کوچکترین عدد فرد – بزرگترین عدد فرد) = تعداد اعداد فرد
مثال: از عدد 45تا 158چند عدد زوج وچند عدد فرد وجود دارد؟
57= 1 + 2 ÷ (46 – 158 ) = تعداد اعداد زوج
57 = 1 + 2 ÷ ( 45 – 157 )= تعداد اعداد فرد
------------------------------------------------------------------------------------------------------------------------------------------------------------
مجموع اعداد صحیح متوالی
1-برای محاسبهی مجموع اعداد صحیح متوالی،از فرمول زیر استفاده میشود.
2 ÷ (تعداد اعداد × مجموع عدد اولی وعدد آخری ) = مجموع اعداد صحیح متوالی
مثال: محموع اعداد صحیح از 1 تا 100 را به دست آورید؟
مجموع اعداد 5050 = 2 ÷ 100( × (100 + 1 ))
2- برای محاسبه مجموع اعداد صحیح فرد متوالی که از عدد(یک) شروع
میشوندویا مجموع اعداد صحیح زوج متوالیکهازعدد(دو)شروع میشوند
علاوه بر فرمول قبلی،میتوانیم از فرمول های زیر استفاده کنیم.
تعداد اعداد × تعداد اعداد = مجموع اعداد صحیح فرد متوالی
(1 + تعداد اعداد) × تعداد اعداد = مجموع اعداد صحیح زوج متوالی
مثال: مجموع اعداد صحیح زوج و مجموع اعداد صحیح فرد متوالی از 1 تا100 را به دست آورید؟
از 1 تا 100 ، 50تا فرد و 50 تا زوج هستند.
2500 = 50 × 50 = تعداد اعداد صحیح فرد متوالی
2550 = 51 × 50 = تعداد اعداد صحیح زوج متوالی
عدد وسطی
هرگاه مجموع چند عدد صحیح متوالی (با فاصله های یکسان) را بدهند و آن اعداد را بخواهند ،مجموع آن اعداد را بر تعدادشان تقسیم کرده،عدد وسطی به دست میآید.
1- اگر تعداد اعدادفرد باشد مانندمثال زیر عمل،می کنیم.
مثال: مجموع 5 عدد صحیح متوالی 75 میباشدکوچکترین عدد را به دست آورید؟
عدد وسطی 15 = 5 ÷ 75
75 = 17 + 16 + 15 + 14 + 13
2- اگر تعداد اعداد زوج باشد مانند مثال زیر عمل می کنیم.
مثال: مجموع 6 عدد صحیح فرد متوالی 96 می باشد یزرگ ترین عدد را به دست آورید؟
عدد وسطی 16 = 6 ÷ 96
رقم یکان
1- هرگاه چند عدد زوج را با هم جمع کنیم رقم یکان حاصل جمع،حتماً زوج خواهد شد.
2- هرگاه چند عدد فرد را با هم جمع کنیم رقم یکان حاصل جمع،ممکن است زوج باشد یا فرد.
اگر تعداد اعداد،فرد باشد رقم یکان حاصل جمع،فرد میشود و بلعکس
3-هرگاه عدد زوجی را هرچند بار در خودش ضرب کنیم رقم یکان حاصل ضرب،حتماً زوج خواهد بود.
کسر بین دو کسر
برای نوشتن کسر بین دو کسر،کافی است صورتها را با هم و مخرجها را نیز را باهم جمع کرد به مثال زیر توجه کنید.
سه کسر بین دو کسر نوشته شده است.
بخش پذیری
بخش پذیری بر 11 : از سمت چپ شروع می کنیم و ارقام را یکی در میان با هم جمع می کنیم و بعد حاصل را از هم کم میکنیم و حاصل تفریق را بر 11 تقسیم میکنیم،اگر باقی مانده صفر شود بر 11 بخش پذیر است.
مثال: آیا عدد 32121456 بر 11 بخشپذیر است؟
تقسیم کسرها:
تقسیم کسرها را به سه روش زیر، می توانیم انجام دهیم.
1- اگر مخرجها مساوی باشند از مخرجها صرف نظر کرده صورت کسر اول را بر صورت کسر دوم تقسیم میکنیم.
اما اگر مخرجها مساوی نباشند مخرج مشترک گرفته و مخرجها را مساوی میکنیم سپس صورت کسر اول را بر صورت کسر دوم تقسیم میکنیم.
2- کسر اول را نوشته، علامت تقسیم را به ضرب تبدیل کرده و سپس کسر دوم را معکوس می کنیم و عمل ضرب را انجام می دهیم.
3- دور در دور و نزدیک در نزدیک: از این روش، فقط در مواقعی که لازم باشد استفاده می کنیم.
نسبت و تناسب :
1- تناسب زمانی : در این نوع تناسب، زمان تغییری نمی کند.
مثال : اگر 4 پیراهن روی طناب در مدت زمان یک ساعت خشک شوند 8 پیراهن در همان شرایط در همان یک ساعت خشک می شود.
2- تناسب مستقیم : اگر قیمت یک تخم مرغ 100 تومان باشد 5 تخم مرغ 500 تومان می شود یعنی با افزایش تعداد تخم مرغ ها، قیمت خرید تخم مرغ ها نیز به همان نسبت افزایش می یابد.
3- تناسب معکوس : گاهی اوقات کمیت ها با هم نسبت عکس دارند یعنی هرچه یکی را زیاد کنیم به همان نسبت ، دیگری هم کم می شود. در این حالت می گوییم تناسب معکوس است. مثلاً اگر2 کارگر، کاری را در مدّت 6 روز انجام می دهند ،4 کارگر، همان کار را در مدت 3 روز انجام می دهند.
زاویهی بین دو عقربهی ساعت شمار و دقیقه شمار:
برای محاسیه زاویهی بین دو عقربهی ساعت شمار و دقیقه شمار ، مقدار ساعت را در عدد 30 ضرب کرده، مقدار دقیقه را در عدد5/5 ضرب کرده، عدد کوچک تر را از عدد بزرگ تر کم می کنیم. در صورتی که جواب به دست آمده از 180 درجه بیشتر باشد آن را از 360 کم می کنیم.
مثال: زاویه ای که دو عقربه ی ساعت شمار و دقیقه شمار در ساعت 1:50 می سازند چند درجه است؟
زاویهی بین دو عقربه
مجموع زوایای داخلی چند ضلعی ها:
برای این که مجموع زاویه های داخلی هر چند ضلعی رامحاسبه کنیم ، تعداد ضلع ها را منهای 2 نموده ، در 180 ضرب می کنیم.
180 × (2 – تعداد ضلع ها ) = مجموع زاویه های داخلی
مثال : مجموع زاویه های داخلی یک 5 ضلعی را به دست آورید؟
درجه 540 = 180× (2 – 5 ) : پنج ضلعی
تعداد قطرهای چندضلعی ها:
از تعداد ضلع ها، 3 تا کم کرده، جواب را در تعداد ضلع ها ضرب کرده و سپس جواب را بر 2 تقسیم می کنیم.
2÷ تعداد ضلع ها × ( 3 - تعداد ضلع ها ) = تعداد قطرها
از هر راس چند ضلعی به اندازهی (3- تعدا ضلع ها ) قطر می گذرد. مثلا از یک راس چهار ضلعی ( 1= 3 – 4) یک قطر می گذرد.
مثال : یک شش ضلعی چند قطر دارد؟
تعداد قطرها 9= 2 ÷ 6 × ( 3 – 6 )
تعداد زاویه ها:
هرگاه در چند زاویه ی مجاور که دارای راس مشترک هستند ، بخواهیم تعداد زاویه ها را تعیین کنیم ، از فرمول زیر استفاده می کنیم.
2 ÷ (تعداد فاصله ها× تعداد نیم خط ها ) = تعداد زاویه ها
توجه : تعداد فاصله ها،از تعداد نیم خط ها یکی کم تر است.
مثال : در شکل روبرو چند زاویه وجود دارد؟
ارتفاع وارد بر وتر:
برای محاسبه ارتفاع وارد بر وتر ، می توانیم از فرمول زیر استفاده کنیم.
وتر ÷ حاصل ضرب دو ضلع زاویهی قائمه= ارتفاع واردبر وتر
مثال : اگر دو ضلع زاویهی قائمه مثلث قائم الزاویهای 5 و 12 س باشدووتر آن 15 س باشد.طول ارتفاع وارد بر وتر آن چقدر است؟
برای مشاهده ی فرمول های ریاضی برای آزمون تیز هوشان ومدارس نمونه دولتی به ادامه ی مطلب توجه کنید
فرمول مساحت و محیط اشکال هندسی
مساحت مـــربع = یـــک ضلع × خـــودش
محیــط مـــربــــع = یک ضلع × 4
2) مساحت مسـتطیـــــــل = طـول × عـرض
محیط مستطیل = ( طول + عرض) × 2
3) مساحت مثلث = ( قاعده × ارتــــــفاع ) ÷ 2
محیط مثلث = مجموع سه ضلع
4) مساحت مثلث متساوی الاضلاع = ( قاعده × ارتفاع ) ÷ 2
محیط مثلث متساوی الاضلاع = یک ضلع × 3
5) مساحت مثلث متساوی الساقین = ( قاعده × ارتفاع ) ÷ 2
محیط مثلث متساوی الساقین= مجموع سه ضلع
6) مساحت مثلث قائم الزاویه = ( قاعده × ارتفاع ) ÷ 2
محیط مثلث قائم الزاویه = مجموع سه ضلع
7) مساحت ذوزنقه = ( قاعده بزرگ + قاعده کوچک ) × ارتفاع ÷ 2
محیط ذوزنقه = مجموع چهار ضلع
8) مساحت لوزی = ( قطر بزرگ × قطر کوچک ) ÷ 2
محیط لوزی = یک ضلع × 4
9) مساحت متوازی الاضلاع = قاعده × ارتفاع
محیط متوازی الاضلاع = مجموع دو ضلع متوالی × 2
10) مساحت دایره = عدد پی ( 3/14 ) × شعاع × شعاع
محیط دایره = عدد پی ( 3/14 ) × قطر
11) مساحت کره = 4 × 3/14 × شعاع به توان دو
حجم کره = چهار سوم × 3/14 × شعاع به توان سه
12) مساحت بیضی = (نصف قطر بزرگ × نصف قطر کوچک ) × 3/14
13 ) محیط چند ضلعی منتظم = یک ضلع × تعداد اضلاعش
14 ) حجم مکعب مستطیل = طـول × عـرض × ارتفاع
حجم مکعب مربع = قاعده × ارتفاع ( طول یال×مساحت یک وجه)
15 ) حجم هرم = مساحت قاعده ی هرم × ارتفاع هرم× یک سوم
16) مساحت جانبی استوانه = محیط قاعده × ارتفاع حجم استوانه = مساحت قاعده × ارتفاع
سطح کل استوانه = سطح دو قاعده + مساحت جانبی ( مساحت مجموع دو قاعده + ارتفاع × پیرامون قاعده )
17) مساحت جانبی منشور = مجموع مساحت سطوح جانبی
مساحت کلی منشور = مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی
18) حجم مخروط = مساحت قاعده × یک سوم × ارتفاع
منبع :خانه ی ریاضی و فیزیک
فرمول شیمیایی
|
|
ممکن است این مقاله نیازمند ویکیسازی باشد تا با استانداردهای کیفی ویکیپدیا همخوانی یابد. خواهشمندیم با افزودن پیوندهای داخلی مرتبط، یا با بهبود چیدمان به بهبود آن کمک کنید. |
فرمول شیمیایی و یا فرمول مولکولی یک راه برای بیان اطلاعات مربوط به اتمهای تشکیل دهنده یک ترکیب شیمیایی خاص است. با تکیه بر فرمول تجربی به تنهایی، یک مولکول متان برای مثال ممکن است شامل یک کربن و چهار هیدروژن یا دو کربن و هشت هیدروژن با هر مضربی از CH۴ باشد. ما باید فرمول مولکولی یعنی:فرمولی که شمار واقعی هر نوع اتم را در یک مولکول نشان دهد را نیز باید پیدا کنیم.
برای پیدا کردن فرمول مولکولی باید وزن مولکولی را تعیین کنیم، امروزه وزن مولکولی را با طیف سنجی جرمی که به طور مطمئن مقدار دقیق آن را به دست میدهد اندازه میگیرند برای مثال اتان دارای فرمول تجربی CH۳ است برای آن وزن مولکولی ۳۰ به دست میآید که نشان میدهد از میان فرمولهای مولکولی ممکن فرمول صحیح باید C۲H۶ باشد.
منابع
- کتاب شیمی آلی ۱ نوشته تورنتون موریسون و نیلسون بوید مترجمان: دکتر علی سیدی اصفهانی، دکتر عیسی یاوری و دکتر احمد میرشکرائی صفحهٔ ۸۸
[نمایش]
ترکیبات سدیم
لگاریتم
لُگاریتم یک عدد در یک پایه، برابر با توانی از پایهاست که آن عدد را میدهد. برای نمونه لگاریتم ۱۰۰۰ در پایهٔ ۱۰، برابر با ۳ است. چون ۱۰ × ۱۰ × ۱۰ = ۱۰۰۰ یا به بیان کلیتر اگر x = by باشد آنگاه لگاریتم x در پایهٔ b برابر با y خواهد بود و به زبان ریاضی آن را به صورت  نمایش میدهیم. مانند:
نمایش میدهیم. مانند: 
لگاریتم نخستین بار از سوی جان نپر در اوایل سده ۱۷ میلادی به عنوان وسیلهای برای آسان تر کردن محاسبات، معرفی شد؛ که به سرعت از سوی دانشمندان و مهندسان پذیرفته شد و برای آسانتر کردن و سریعتر کردن محاسبه جدولهای لگاریتم اعشاری و ایجاد شدند و مورد استفاده قرار گرفتند. تمامی این ابزارها بر پایهٔ این مفهوم که «لگاریتم حاصل ضرب برابر است با مجموع لگاریتمها»، ساخته شده بودند:
مفهوم امروزی لگاریتم از تلاشهای لئونارد اویلر در قرن ۱۸ گرفته شده است؛ او توانست مفهوم لگاریتم را با مفهوم تابع نمایی پیوند دهد.
لگاریتم در پایهٔ ۱۰ را لگاریتم اعشاری مینامند که کاربرد بسیار زیادی در مهندسی دارد. لگاریتم در مبنای ثابت e یا عدد نپر ≈ ۲٫۷۱۸ را لگاریتم طبیعی مینامند. این لگاریتم در ریاضیات محض بویژه حساب دیفرانسیل و انتگرال بسیار کاربرد دارد. نیز در مبنای ۲ نوشته میشود و کاربرد زیادی در علوم رایانه دارد.
به کمک مقیاس لگاریتمی، میتوان اندازههای بسیار بزرگ را در ابعاد بسیار کوچکتری نشان داد برای نمونه دسیبل یکایی لگاریتمی است که برای نشان دادن و نسبت ولتاژ کاربرد دارد. در شیمی نیز پ هاش که معیاری برای نشان دان میزان اسیدی بودن مایعات است در مقیاس لگاریتمی بیان میشود. همچنین لگاریتم در نظریهٔ پیچیدگی محاسباتی و در برخی شکلهای هندسی مانند برخالها کاربرد دارد. از دیگر کاربردهای آن میتوان به فاصله در موسیقی و رابطههای شمارش اعداد اول اشاره کرد.
تابع توان وارون تابع لگاریتم است و لگاریتم مختلط، تابع وارون تابع نمایی به کار رفته در اعداد مختلط است. لگاریتم گسسته نیز در رمزنگاری کلید عمومی استفاده میشود.
محتویات |
انگیزهٔ اولیه و تعریف
انگیزهٔ ساخت لگاریتم، داشتن وارون تابع توان بودهاست. برای نمونه، توان سوم ۲، ۸ است چون ۸ = ۲ × ۲ × ۲ = ۲۳ پس لگاریتم ۸ در پایهٔ ۲، ۳ میشود.
به توان رساندن
توان سوم عددی مانند b برابر است با 3 بار ضرب b در خودش. حال اگر b به توان یک عدد طبیعی مانند n برسد به معنی n بار ضرب کردن b در خودش است که به صورت زیر نمایش میدهیم:
در صورتی که n عدد طبیعی نباشد، آنگاه bn جواب دیگری خواهد داشت. مانند 1- که b-1 برابر معکوس b است.[nb ۱]
تعریف
لگاریتم عددی مانند y در پایهٔ b عبارت است از یافتن عددی که اگر b به توان آن عدد برسد برابر با y شود. به عبارت دیگر جواب x معادلهٔ زیر برابر با لگاریتم y در پایهٔ b خواهد بود.[۲]
پایهٔ b باید یک عدد حقیقی y نیز باید یک عدد مثبت باشد.[۲]
چند نمونه
- نمونهٔ یکم
برای نمونه ۴ = (۱۶) log۲ چون ۱۶ = ۲ × ۲ × ۲ × ۲ = ۲۴
- نمونهٔ دوم
برای توانهای منفی نیز لگاریتم معتبر است مانند:
چون
- نمونهٔ سوم
(۱۵۰) log۱۰ تقریباً برابر است با ۲٫۱۷۶ عددی میان ۲ و ۳ چون ۱۵۰ خود عددی است میان ۱۰۰ = ۱۰۲ و ۱۰۰۰ = ۱۰۳ همچنین در هر پایهای  و
و  چون به ترتیب:
چون به ترتیب: 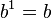 و
و  است.
است.
قوانین لگاریتم
رابطههای مختلفی به عنوان قوانین لگاریتم وجود دارند که میتوانند میان فرمولهای لگاریتمی رابطه برقرار کنند.
ضرب، تقسیم، توان، ریشه
لگاریتم حاصل ضرب چند عدد برابر است با مجموع لگاریتمهای تک تک آن عددها. لگاریتم نسبت دو عدد (تقسیم) برابر است با تفاضل لگاریتم آن دو عدد. لگاریتم توان p ام یک عدد برابر است با p برابر لگاریتم آن عدد. لگاریتم ریشهٔ p ام یک عدد برابر است با لگاریتم آن عدد تقسیم بر p. جدول زیر قوانین لگاریتم را همراه با یک نمونه نشان دادهاست:
| رابطه | نمونه | |
|---|---|---|
| ضرب |  |
 |
| تقسیم |  |
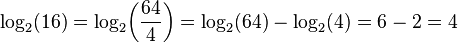 |
| توان | 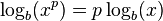 |
 |
| ریشه | ![log_b sqrt[p]{x} = frac {log_b (x)} p ,](http://upload.wikimedia.org/math/3/c/a/3ca49ea6d6cf9ced59d76f8fc5e42755.png) |
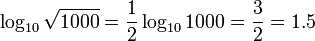 |
تغییر پایه
میتوان 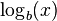 را به صورت غیر مستقیم با گرفتن لگاریتم x و b در یک پایهٔ دلخواه مانند k بدست آورد، به این ترتیب که:
را به صورت غیر مستقیم با گرفتن لگاریتم x و b در یک پایهٔ دلخواه مانند k بدست آورد، به این ترتیب که:
بیشتر ماشین حسابهایی که در دسترس اند لگاریتم را تنها در مبنای ۱۰ و عدد نپر[۳] محاسبه میکنند و لگاریتم در پایههای دیگر را به کمک رابطهٔ بالا محاسبه میکنند:
همچنین اگر عددی مانند x و مقدار لگاریتم آن را در یک مبنای نامشخص b داشته باشیم 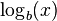 حال میتوان مبنای نامشخص b را به ترتیب زیر محاسبه کرد:
حال میتوان مبنای نامشخص b را به ترتیب زیر محاسبه کرد:
پایههای ویژه
پایههای ویژهٔ لگاریتم عبارتند از ۱۰، ۲ و عدد e (عدد گنگی تقریباً برابر با ۲٫۷۱۸۲۸) در آنالیز ریاضی لگاریتم در پایهٔ عدد e بسیار کاربرد دارد، لگاریتم در پایهٔ ۱۰ را میتوان بوسیلهٔ ماشین حسابهای دستی که در اختیار است به آسانی محاسبه کرد:[۴]
لگاریتم در پایهٔ ۱۰ را میتوان به آسانی با شمردن تعداد رقمهای یک عدد بدست آورد. برای نمونه (۱۴۳۰) log۱۰ تقریباً برابر است با ۳٫۱۵ چون ۱۴۳۰ چهار رقم دارد پس لگاریتم آن در پایهٔ ۱۰ باید عددی میان ۳ و ۴ باشد. لگاریتم در پایهٔ ۲ در علوم رایانه مورد استفاده قرار میگیرد چون در آن از دستگاه اعداد دودویی استفاده میشود.
جدولی که در ادامه قرار داده شدهاست علامتهایی که برای نشان دادن تابع لگاریتم کاربرد دارند و جایی که هر نوع لگاریتم مورد استفاده قرار میگیرد را نشان دادهاست. در بسیاری موارد اگر بتوان از روی نوشته تشخیص داد تنها از نماد لگاریتم استفاده میکنند و از نوشتن پایهٔ آن خودداری میکنند. در جدول زیر نمادی ستون «نماد ISO» مربوط به پیشنهادی است که از سوی سازمان بینالمللی استانداردسازی[۵] داده شدهاست.(ISO 31-11)
| پایهٔ b | نام گونهٔ لگاریتم | ISO نماد در | دیگر نمادها | کاربرد |
|---|---|---|---|---|
| ۲ | lb(x)[۶] | ld(x)، log(x) (در علوم رایانه)، lg(x) |
علوم رایانه، نظریهٔ اطلاعات | |
| e | لگاریتم طبیعی | ln(x)[nb ۲] | log(x) (در ریاضی و بسیاری از زبانهای برنامه نویسی[nb ۳]) |
آنالیز ریاضی، فیزیک، شیمی آمار, علم اقتصاد, و بعضی از زمینههای مهندسی |
| ۱۰ | لگاریتم اعشاری | lg(x) | log(x) (در مهندسی، زیست شناسی، اخترشناسی), |
در زمینههای گوناگون مهندسی (مانند دسیبل)، تهیه جدول لگاریتم و ماشین حسابهای مهندسی |
پیشینه
پیشینیان
از کسانی بود که با مفهومی به نام ardhaccheda کار کرد. ardhaccheda یعنی تعداد دفعاتی که میتوان ۲n را نصف کرد. برای نمونه برای توانهای دقیق ۲ این کار برابر با لگاریتم گرفتن در مبنای ۲ بود؛ وی همچنین لگاریتم در پایهٔ دیگر اعداد صحیح مانند لگاریتم در پایهٔ ۳ (trakacheda) و در پایهٔ ۴ (caturthacheda) را نیز معرفی کرد.[۱۰][۱۱] در سال ۱۵۴۴ میلادی در نورنبرگ Arithmetica integra را منتشر کرد، در این نوشته جدولی از اعداد صحیح و توانهای ۲ داده شده بود، این جدول به عنوان نسخهٔ اولیهٔ جدول لگاریتم شمرده میشود.[۱۲][۱۳]
از نپر تا اویلر

روش لگاریتمگیری در سال ۱۶۱۴ از سوی جان نپر در کتابی با عنوان Mirifici Logarithmorum Canonis Descriptio (توصیفی بر قانون شگفتانگیز لگاریتم) ارائه شد.[۱۴] همچنین (به فرانسوی: Joost Bürgi) نیز جداگانه روش لگاریتمگیری را پیدا کرده بود اما آن را شش سال پس از نپر منتشر کرد.[۱۵]
نپر، با استفاده از روش تقسیمهای متوالی توانسته بود عبارت  را به ازای Lهای میان ۱ تا ۱۰۰ محاسبه کند. جواب این عبارت برای ۱۰۰ = L تقریباً برابر است با ۰٫۹۹۹۹۹ = ۱ - ۵-۱۰ و ۲۰ ۰٫۹۹۵ ≈ ۰٫۹۹. این محاسبات که ۲۰ سال طول کشید، باعث شد تا او بتواند به ازای هر عدد N در بازهٔ ۵ تا ۱۰ میلیون، بتواند عدد L را پیدا کند که در رابطهٔ زیر صدق کند:
را به ازای Lهای میان ۱ تا ۱۰۰ محاسبه کند. جواب این عبارت برای ۱۰۰ = L تقریباً برابر است با ۰٫۹۹۹۹۹ = ۱ - ۵-۱۰ و ۲۰ ۰٫۹۹۵ ≈ ۰٫۹۹. این محاسبات که ۲۰ سال طول کشید، باعث شد تا او بتواند به ازای هر عدد N در بازهٔ ۵ تا ۱۰ میلیون، بتواند عدد L را پیدا کند که در رابطهٔ زیر صدق کند:
نپر ابتدا نام «عدد ساختگی» را بر L نهاد ولی پس از مدتی واژهٔ «لگاریتم» logarithm را معرفی کرد و آن را بر عددی گذاشت که نمایندهٔ یک نسبت است: واژهٔ λόγος برابر logos به معنی «نسبت» است و واژهٔ ἀριθμός برابر arithmos به معنی «عدد» است. بوسیلهٔ عبارت زیر میتوان مفهوم پیشین لگاریتم را با مفهوم امروزی لگاریتم طبیعی مرتبط کرد:[۱۶]
با تقریب خوبی داریم:
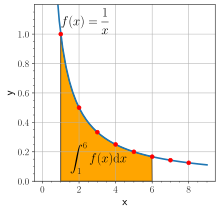
این دستآورد خیلی زود مورد تحسین گستردهٔ دیگران قرار گرفت، به همین دلیل با تلاش دانشمندانی چون (Bonaventura Cavalieri) از ایتالیا، (Edmund Wingate) از فرانسه، زو فنگزوئو (Xue Fengzuo) از چین و... مفهوم لگاریتم همه جا فراگیر شد.[۱۷]
در سال ۱۶۴۷ توانست مفهوم لگاریتم را با یک چهارم هذلولی مرتبط کند، با فرض آنکه سظح  زیر منحنی هذلولی به ازای ۱ = x تا t در رابطهٔ زیر صدق میکند:
زیر منحنی هذلولی به ازای ۱ = x تا t در رابطهٔ زیر صدق میکند:
لگاریتم طبیعی اولین بار از سوی در مقالهٔ Logarithmotechnia که در سال ۱۶۶۸ منتشر کرد، توضیح داده شد.[۱۸] البته پیش از او جان اسپیدل که یک معلم ریاضی بود در سال ۱۶۱۹ جدولی از لگاریتم طبیعی را گردآوری کرده بود.[۱۹] در حدود سال ۱۷۳۰ لئونارد اویلر تابع نمایی و لگاریتم طبیعی را به گونهٔ زیر تعریف کرد:
همچنین اویلر نشان داد که این دو تابع وارون یکدیگرند.[۲۰][۲۱][۲۲]
جدول لگاریتم، خطکش لغزان و کاربردها در گذشته

با ساده سازی محاسبات پیچیده، از لگاریتم میتوان در دانش پیشرفته مانند اخترشناسی، نقشه برداری، هوانوردی و ... کمک گرفت. پیر سیمون لاپلاس دربارهٔ لگاریتم گفتهاست:
وسیلهای ستودنی است که به کمک آن کار چند ماه به چند روز کاهش مییابد، عمر اخترشناسان را دو برابر میکند و از خطاهای کوچک میگذرد و از جملههای طولانی و جدانشدنی ریاضی بیزار است.
وسیلهٔ کلیدی که پیش از در دسترس قرار گرفتن ماشین حساب و رایانه برای محاسبهٔ لگاریتم از آن استفاده میشد و بوسیلهٔ آن بود که ارزش لگاریتم روشن شد، جدول لگاریتم بود.[۲۴] چنین جدولی برای اولین بار بوسیلهٔ در سال ۱۶۱۷ بلافاصله پس از ابتکار نپر ایجاد شد. پس از آن جدولهای وسیع تر و دقیق تری نوشته شد. در این جدولها مقدار 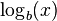 و
و 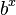 برای هر عدد x در یک بازهٔ مشخص با دقت مشخص و برای پایههای مشخص (معمولاً پایهٔ ۱۰) نوشته شده بود. برای نمونه در اولین جدول بریگز، لگاریتم طبیعی اعداد صحیح میان ۱ تا ۱۰۰۰ با دقت ۸ رقم اعشار نوشته شده بود. از آنجایی که تابع
برای هر عدد x در یک بازهٔ مشخص با دقت مشخص و برای پایههای مشخص (معمولاً پایهٔ ۱۰) نوشته شده بود. برای نمونه در اولین جدول بریگز، لگاریتم طبیعی اعداد صحیح میان ۱ تا ۱۰۰۰ با دقت ۸ رقم اعشار نوشته شده بود. از آنجایی که تابع 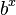 وارون
وارون
قضیه فیثاغورس
قضیهٔ فیثاغورس در هندسه و فضای اقلیدسی بخشی از صورت کلی قانون کسینوسها هنگامی که زاویهٔ بین دو بردار ۹۰ درجهاست میباشد. این قضیه به نام ریاضیدان یونانی فیثاغورس نامگذاری شدهاست. به سخن دیگر در یک مثلث راستگوشه (قائم الزاویه) همواره مجموع توانهای دوم دو ضلع برابر با توان دوم ضلع سوم است.
قانون کسینوسها بیان میکند که اگر دو بردار (یا خط) a و b در راس O تشکیل یک زاویه با نام A بدهند بردار مجموع از رابطهٔ  بدست میآید.
بدست میآید.
همانطور که میبینید هر گاه زاویه A برابر با ۹۰ درجه باشد مقدار  صفر شده و در نتیجه صورت قضیهٔ فیثاغورس بدست میآید:
صفر شده و در نتیجه صورت قضیهٔ فیثاغورس بدست میآید:

وارون این قضیه نیز درست است، به عبارت دیگر، اگر  باشد، مثلث قائمالزاویه است. اثبات عکس قضیه فیثاغورس را به اقلیدس نسبت دادهاند.[۱]
باشد، مثلث قائمالزاویه است. اثبات عکس قضیه فیثاغورس را به اقلیدس نسبت دادهاند.[۱]
محتویات |
نمایشهای دیگر
اگر c طول وتر مثلث راستگوشه باشد و a و b طول دو ضلع دیگر آن، قضیهٔ فیثاغورس را به شکل رابطهٔ زیر مینویسیم:
و اگر مقدار a و b معلوم باشد c را به این شکل بدست میآوریم:
و اگر c معلوم باشد و یکی از دو ضلع a یا b نامعلوم، آنها را اینگونه بدست میآوریم:
یا
همانگونه که در پیشگفتار بیان شد، قضیهٔ فیثاغورس بخشی از صورت کلی قانون کسینوسها است.
فرمولها و راهنمای ریاضی ششم ابتدایی
1-هرگاه چند نقطهی متمایز(جدا از هم)،بر روی یک خط راست باشند تعداد پاره خط ها از فرمول زیر به دست می آید.
2 ÷ (تعداد فاصله ها × تعداد نقطه ها ) = تعداد پاره خط ها
توجه : تعداد فاصلهها همیشه یکی کمتر از تعداد نقطهها است.
2-هرگاه چند نقطهی متمایز،بر روی خط راست باشند، تعداد نیم خطها از فرمول زیر،به دست می آید.
2 × تعداد نقطهها = تعداد نیم خطها
3-هرگاه چند نقطهی متمایز، برروی یک نیم خط باشند،تعداد نیم خطها مانند مثال زیر به دست میآید.
مثال: برروی یک نیم خط،هفت نقطهی متمایز وجود دارد چند نیم خط،در شکل وجود دارد؟
پس (8 = 1 + 7 ) نقطه داریم یعنی 8 نیم خط خواهیم داشت.
4- هرگاه چند نقطهی متمایز، برروی یک پاره خط باشند نیم خطی، درشکل وجود ندارد.
برش و قسمت:
وقتی می خواهیم یک قطعه یا جسمی رشته مانند را به قسمت های مساوی ویا نامساوی تقسیم کنیم همیشه تعداد قسمتها یکی بیشتر از تعداد برشها است.
مثال: یک آهنگر , میله ای به طول 12 متر را به چهار قسمت تقسیم کرد او برای این کار چند برش زده است؟
برش 3 = 1 – 4 (قسمت)
مجموع و اختلاف:
هرگاه مجموع دو عدد و اختلاف آن دو عدد را به ما بدهند و آن دو عدد را از ما بخواهند، از دو راه زیر به دست میآید.
1-اگر مجموع واختلاف را از هم کم کرده،بر2 تقسیم کنیم عدد کوچکتر به دست میآید.
2- اگر مجموع واختلاف را با هم جمع کرده،بر2 تقسیم کنیم عدد بزرگتربه دست میآید.
تعداد یک رقم در یک مجموعهی اعداد متوالی
هرگاه چند نقطهی متمایز(جدا از هم)،بر روی یک خط راست باشند تعداد پاره خط ها از فرمول زیر به دست می آید.
اگر می خواهید با موتور جست و جو گر هوشمند ایرانی آشنا شوید کافیست روی ادامه ی مطلب کلیک کنید.