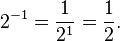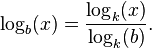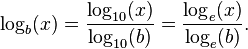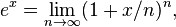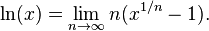نام بازی: Neighbours From Hell Pack
پلتفورم : pc
ژانر: Strategy
تاریخ انتشار جهانی :
تاریخ انتشار در آمریکا :
تاریخ انتشار در اروپا :
نوع فایل : Collection Games
زبان: English
فرمت ایمیج: ISO
ناشر: Encore Software, Inc
مد بازی : مولتی پلیر
حمایت توسط : JoWood Productions
درجه بندی سنی : PEGI: 3+
قابلیت آنلاین:دارد

داستان بازی Grand Theft Auto IV در زمان کنونی یعنی در سال 2007 و در Liberty City به وقوع می پیوندد . شهری که شبیه سازی شده از شهر نیویورک آمریکاست . قهرمان این نسخه Niko Bellic نام دارد . او فردی اهل اروپای شرقی می باشد و در کشور خود در کار قاچاق انسان بوده است
داستان بازی Grand Theft Auto IV در زمان کنونی یعنی در سال 2007 و در Liberty City به وقوع می پیوندد . شهری که شبیه سازی شده از شهر نیویورک آمریکاست . قهرمان این نسخه Niko Bellic نام دارد . او فردی اهل اروپای شرقی می باشد و در کشور خود در کار قاچاق انسان بوده است اما او دیگر از این کار خسته شده است و قصد دارد تا زندگی تازه ای را آغاز کند و این در حالی بود که Roman ، پسر عموی Niko نیز که در Liberty City زندگی می کرد با فرستادن E-mail های متعدد از او دعوت می کرد که به آنجا برود . Roman به Niko می گفت که در Liberty City من به همه ی خواسته ها و آرزوهایم رسیده ام و اکنون 15 ماشین اسپرت و دو زن و ثروت فراوانی دارم . Niko هم که قصد داشت تا زندگی جدیدی را شروع کند و گذشت ی سیاهش را از یاد ببرد به امید گفته های Roman به Liberty City سفر کرد و در آنجا Roman را یافت و فهمید که Roman یک راننده تاکسی ساده بیش نیست و در محله ی نسبتآ فقیر نشین Broker زندگی می کند . بله ، Roman به او دروغ بزرگی گفته بود چراکه او نه تنها زندگی خوب و راحتی نداشت ، بلکه دارای قرض و گرفتاری های فراوانی نیز بود و گروه های مختلف تبهکاران Liberty City خصوصآ مافیای روسیه هم برای او مشکلات جانی و مالی زیادی به وجود آورده بودند و Roman از دست آن ها امنیت نداشت . Roman برای مقابله با تمام این مشکلات نیاز به یک پشتیبان داشت تا بتواند آن ها را رفع کند و با توجه به شناختی که از Niko و توانایی هایش داشت ، او را بهترین پشتیبان و کمک کننده ی خود می دانست و به همین جهت به Niko چنین دروغی را گفت تا او را به آنجا بکشاند . Niko هم که دیگر در مقابل یک عمل انجام شده قرار گرفته بود و راهی هم برای برگشت نداشت باید با مشکلات جدیدش دست و پنجه نرم می کرد و زندگی تازه اش را با وجود این مشکلات آغاز می نمود . او برای رفع این مشکلات نیاز به پول داشت و برای دستیابی به پول می بایست بار دیگر به جرم و جنایت دست بزند و اینجاست که داستان هیجان انگیز بازی آغاز می شود . اگر تا به حال Grand Theft Auto IV را بازی نکرده اید بدانید که یکی از بهترین بازیهای امسال را را از دست داده اید.در تصدیق این مطلب می توان به نظر تعداد زیادی از منتقدین بازی های ویدئویی از سرتاسر دنیا اشاره کرد که در نقدهای خود امتیاز کامل را به GTA IV اختصاص دادند.در این مقاله فرض کرده ایم که شما با GTA IV و ویژگی های مخصوص آن آشنا هستید و قصد داریم بررسی کنیم که آیا نسخه ی PC بازی برترین نسخه ی GTA IV خواهد بود ویا خیر. ما هر دو نسخه ی Xbox360 و PS3 بازی را قبلا تجربه کرده ایم ولی باید گفت نسخه ی PC الحق و الانصاف چیز دیگری است.در نسخه ی PC با توجه به قدرت پردازش بالا ساختمان های بیشتری را در پیش زمینه خواهید دید که باعث می شود فضای شهر Liberty City شکل واقعی تر به خود بگیرد و شلوغی شهر را کاملا احساس کنید.همچنین قدرت پردازش PC باعث شده وسایل نقلیه بیشتری در خیابان های شهر رفت و آمد کنند و زمانی که از میان خیابان ها عبور می کنید کاملا ترافیک شهر را احساس خواهید کرد.
حجم فایل : 7.53 مگابایت
دانلود با لینک مستقیم از سرور سایت
پسورد فایل : www.freegames.ir
به بفرما با رمزاش حال کن:
بازدنفلش بالای گوشی موبایل خودش را در می یاره بد این کارم بازم تکرارکن واین شماره هارا وارد کن
در شیمی به هر ترکیب شیمیایی که یک گروهِ هیدرکسیل (-OH) متصل به کربن یک الکل گویند. فرمول کلی یک الکل سادهٔ CnH2n+1OH است. در شیمی الکلها در شمار گروه مهمی از ترکیبهای شیمیایی هستند و در واکنشهای گستردهای شرکت میکنند و بسیاری از ترکیبهای شیمیایی از آنها به دست میآیند، به طوری در کتاب شیمی آلی موریسن و بوید آمدهاست که اگر به شیمیدانی بگویند او را با ده ترکیب شیمیایی دریک جزیره تنها خواهند گذاشت الکل یکی از آنها خواهدبود.
به طور کلی، زمانی که نام الکل به تنهایی به کار میرود، معمولاً منظور اتانول است که همان الکل گرفتهشده از جو یا عرق یا همان مشروبات الکلی میباشد. اتانول مایعی بیرنگ و فرار وبا بویی بسیار تند است که از تخمیر شکرها به دست میآید. همچنین گاه به هر گونه نوشیدنی که الکل داشتهباشد، الکل میگویند. هزاران سال است که معمولاً الکل به عنوان یکی از عاملهای اعتیادآور به شمار میآید.
الکلهای دیگر بیشتر با صفتهای مشخصکنندهٔ ویژهٔ خود میآیند مانند الکل چوب (که همان متانول است) یا ایزوپروپیل الکل. پسوند «ول» نیز در پایان نام شیمیایی همهٔ الکلها میآید.
محتویات |
تاریخچه
الکل را زکریای رازی پزشک ایرانی کشف کرد[نیازمند منبع]
ساختار و دستهبندی
الکلها بسته به نوع کربن[۱] که به گروه OH- پیوند دارد، به سه دسته نوع اول، نوع دوم یا نوع سوم طبقهبندی میشوند: 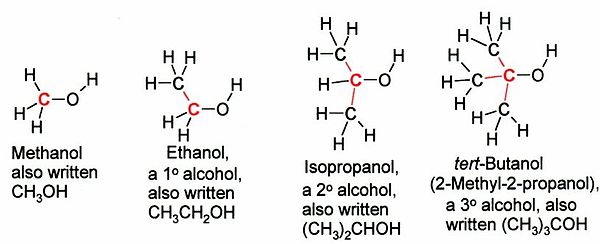
نمایش کلی انواع الکل
- الکل نوع اول CR(H)۲-OH.
- الکل نوع دوم C(R)۲H-OH.
- الکل نوع سومC(R)۳-OH.
خواص فیزیکی الکلها
دمای جوش
الکلها در میان هیدروکربنهای هم وزن خود دمای جوش بالاتری دارند که آن را میتوان به پیوند هیدروژنی الکلها دانست که سبب میشود انرژی بیشتری برای شکستن پیوند بین مولکولی آنها نیاز باشد.
حلالیت
با توجه به این که پیوند بین الکلها مانند آب، پیوند هیدروژنی است به هر اندازهای در آب حل میشود. همچنین با توجه به این که الکلها از یک سو بخشی آلی داشته و از سوی دیگر گروه هیدروکسید دارند بسیاری از مواد آلی را نیز حل میکنند.
محلول ید در محلول آب و الکل را
الکلها بیشتر بویی تند و زننده دارند و اتانول از دوران پیش از تاریخ به دلیلهای گوناگون بهداشتی، رژیمی، مذهبی و تفریحی به عنوان نوشیدنی الکلی به کار میرفتهاست. هرچند استفادهٔ کم و گهگاه الکل میتواند بیزیان باشد، اندازههای بیشتر آن سبب مستی شده و در مقدارهای بیشتر میتواند به اختلالات تنفسی و حتی مرگ نیز بینجامد.[۱] الکلهای دیگر سمیتر از اتانول هستند، که این نیز بیشتر به دلیل نیاز به زمان بیشتر برای تغییر در فرایند سوخت و ساز است و حتی گاه در فرآیندهای دگرگشت(متابولیسم) مادههایی سمی میسازند. برای نمونه متانول، که همان الکل چوب است، به وسیلهٔ آنزیمها در جگر اکسایش مییابد و مادهٔ سمی فرمالدهید تولید میکند که میتواند سبب کوری یا مرگ شود. یکی از راههای کارا در پیشگیری از سمیت فرمالدهید، فراهم آوردن اتانول در کنار آن است چون آنزیمهای هیدروژنزدایی که از متانول فرمالدهید میدهند بر اتانول اثر بیشتری دارند، بدین گونه از پیوند و عمل بر روی متانول پیشگیری میکند. در این زمان متانول باقیمانده وقت دفع از راه کلیهها را پیدا کرده و فرمالدهید باقیمانده نیز به فرمیک اسید تبدیل میشود.سمشناسی
نامگذاری
![]() این بخش از این نوشتار خُرد است. با گسترش آن به ویکیپدیا کمک کنید.
این بخش از این نوشتار خُرد است. با گسترش آن به ویکیپدیا کمک کنید.
در نامگذاری الکلها به روش آیوپاک، تنها در آخر نام آلکان یک «ول» افزوده میشود و زمانی که نیاز ذکر شمارهٔ کربنی که عامل الکلی بر روی آن قرار دارد باشیم، عدد بین نام آلکان و پسوند «ول» قرار میگیرد. مانند «پروپان-1-ول» برای CH3CH2CH2OH و «پروپان-2-ول» برای CH3CH(OH)CH3. 
روشهای فرآوری صنعتی الکلها
از میان روشهای صنعتی الکل میتوان راههای زیر را نام برد:
- آبدارکردن آلکنهای بدست آمده از کراکینگ نفت.
- فرایند السک از آلکنها، مونوکسید کربن و هیدروژن.
- تخمیر کربوهیدراتها.
علاوه بر این سه روش اصلی، روشهای دیگری نیز با کاربرد محدود وجود دارند. بهعنوان مثال، متانول از هیدروژندار کردن کاتالیزوری مونوکسید کربن بدست میآید. مخلوط هیدروژن و مونوکسید کربن با نسبت ضروری، از واکنش آب با متان، آلکانهای دیگر، یا زغال سنگ در دمای بالا بدست میآید.
کاربردها
برخی از کاربردهای الکل:
- سوخت خودرو
- حلال
- کاربردهای پزشکی و گندزدایی ( به دلیل نفوذ فوق العاده به داخل منافذ و حفره ها و از بین بری باکتری های گرم مثبت و منفی و باکتری های مقاوم به اسید با غلظت 70 تا 80 درصد)
- ...
واکنشها
پروتونزدایی
الکلها میتوانند در حضور بازهای بسیار قوی به سان یک اسید عمل کنند و تشکیل یون الکوکسی دهند. برای نمونه در واکنش سدیم هیدروکسید و اتانول، سدیم جانشین هیدروژنِ مثبت(پروتون) الکل شده و سدیم متوکسی به دست میدهد.
هیدروژنزدایی
از راه هیدروژنزدایی الکلها میتوان اتر به دست آورد. 
واکنشهای هستهدوستی
گروه هیدروکسیل الکل یک خوب است و سبب میشود که الکلها بتوانند در واکنشهای هستهدوستی شرکت جویند.
استری شدن
الکل با اسیدهای آلی در محیط اسیدی به آهستگی تشکیل استر میدهد.
اکسایش
الکلهای نوع اول میتوانند در واکنشهای اکسایش تبدیل به آلدهید و پس از آن تبدیل به کربوکسیلیک اسید شوند هرچند که الکلهای نوع دوم در واکنشهای اکسایش تنها تبدیل به کتون میشوند ولی الکلهای نوع سوم در واکنشهای اکسایش شرکت نمیکنند.
الکلهای نوع اول میتوانند بدون واسطه نیز به روشهای زیر به کربوکسیلیک اسیدها تبدیل شوند:
- با حضور پتاسیم پرمنگنات (KMnO4).
- (RuO4).
یک الکل با دو عامل مجاور میتواند در مجاورت سدیم پراکسید(NaIOsub>4) یا (Pb(OAc)4) پیوند کربنش گسستهشده و به دو کربوکسیلیک اسید تبدیل شود.
الکلها و فنولها
اگر گروه هیدروکسیل الکل به کربنی که روی یک است، متصل باشد آنگاه به آن فنول گویند که در دستهٔ دیگری از ترکیبها دستهبندی میشود و ویژگیهای متفاوتی از الکلها دارد.
[نمایش]
| پتاسیم پرمنگنات | |
|---|---|
  |
|
| شناسنامه | |
| نام گذاری آیوپاک | پتاسیم منگنات (VII) |
| نامهای دیگر | پتاسیم پرمنگنات پرمنگنات پرمنگنات پتاسیم |
| فرمول شیمیایی | KMnO4 |
| خواص | |
| جرم مولی | 158.034 گرم بر مول |
| نما (ظاهر) | بلورهای سوزنی بنفش مایل به خاکستری |
| رنگ محلول | در محلول دارای رنگ شدید بنفش است که در غلظتهای چند به رنگ ارغوانی در می آید |
| بو | بدون بو |
| چگالی | 2.703 گرم بر سانتیمتر مکعب |
| دمای ذوب | 240oC همراه با تجزیه شدن |
| حلالیت در آب | 6.38 گرم در 100mL آب (در دمای 20oC) 25 گرم در 100mL آب |
| حلالیت | در الکل و حلالهای آلی دیگر تجزیه می شود. |
| ساختار | |
| ساختار بلوری | دستگاه بلوری اورتورومبیک |
| ترموشیمی | |
| آنتالپی استاندارد تشکیل | 813.4- کیلوزول بر مول |
| 171.7 ژول بر کلوین.مول | |
| خطرات | |
| External MSDS | |
| طبقه بندی EU | اکسید کننده(در استفاده احتیاط کنید) مضر برای سلامتی خطرناک برای محیط زیست |
| لوزی آتش | |
پتاسیم پرمنگنات ترکیبی معدنی است با فرمول شیمیایی KMnO۴. نمک آن از یونهای K+ و MnO۴- تشکیل شده است. سابقاً به آن پرمنگنات و پتاش هم میگفتند. پرمنگنات یک مادهٔ بسیار قوی است. در آب نیز محلول است و محلولی به رنگ ارغوانی تولید میکند که از تبخیر آن بلورهای منشوری و درخشان به رنگ ارغوانی بسیار تیره (مایل به سیاه) بر جای می ماند. در این ترکیب منگنز با عدد اکسایش ۷+ حضور دارد.

محتویات |
ساختار و تهیه
از بلورهایی به شکل اورتورومبیک تشکیل شده که در آن a=910.۵pm و b=572.۰pm و c=742.۵pm است. (a و b و c به ترتیب طول، عرض و ارتفاع دستگاه بلوری اورتورومبیک است.)
همچنین طول پیوند Mn-O در این پیوند برابر ۱۶۲.۹pm است.
تهیهٔ صنعتی پتاسیم پرمنگنات از منگنز دی اکسید است، که خود از سنگ معدن پیرولوسیت به دست می آید. در این روش MnO۲ به دست آمده از پیرولوسیت با پتاسیم هیدروکسید مخلوط شده و در هوا یا در مجاورت پتاسیم نیترات (یک منبع اکسیژن) حرارت داده می شود. در این فرایند پتاسیم منگنات (K۲MnO۴) به دست می آید که در اکسایش الکترولیتی (الکترولیز) در محلول بازی به پتاسیم پر منگنات تبدیل می شود.
| 2 MnO2 + 4 KOH + O2 → 2 K2MnO4 + 2 H2O |
| 2 MnO42– + Cl2 → 2 MnO4– + 2 Cl– |
همچنین پرمنگنات را می توان از اثر دادن سرب دی اکسید (PbO۲) و یا سدیم بیسموتات (NaBiO۳) بر محلول +Mn۲ نیز به دست آورد. از رنگ بنفش روشن حاصل از این واکنش برای تست حضور یا عدم حضور منگنز نیز استفاده می شود.
کاربردها
بسیاری از کاربردهای پتاسیم پرمنگنات بهخاطر خواص اکسیدکنندگی آن است، از اینکه یک اکسید کنندهٔ قوی است و اینکه در این فرایندها محصول فرعی سمی تولید نمی کند. از کاربرد های پرمنگنات پتاسیم می توان به جذب اتیلن اشاره نمود که در پس از برداشت محصولات کشاورزی جهت افزایش عمر انبار مانی می توان اشاره نمود
صنایع سینمایی و تلویزیونی
در صنایع سینمایی و تلویزیونی، پتاسیم پرمنگنات یکی از مواد شیمیایی اصلی برای کهنه کردن مجموعهٔ لباسها و غیره می باشد. خاصیت اکسید کنندگی پرمنگنات باعث میشود که پارچه ها، طناب ها، چوبها و شیشهها بیش از ۱۰۰ سال قدیمی تر از آنچه هستند به نظر بیایند.
از این روش در تهیهٔ فیلمهایی همچون "تروی"، "۳۰۰" و "ایندیانا جونز" استفاده شده است.
تصفیهٔ آب و ضدعفونی
به عنوان یک اکسید کننده، پتاسیم پرمنگنات میتواند به عنوان یک ضد عفونی کننده به کار رود. برای مثال محلول رقیق پرمنگنات برای درمان برخی زخمها مانند عفونت قارچی پا استفاده میشود.
کاربرد دیگر آن حذف آهن و هیدروژن سولفید (مادهٔ حاصل بوی بد تخم مرغ فاسد شده) و حذف فسفر آب آشامیدنیاست.
کاربردهای زیست پزشکی
همانطور که از KMnO۴ برای ضد عفونی کردن آب استفاده می شود، این نمک به طور تخصصی به عنوان ضد عفونی کننده برای درمان برخی بیماریهای انسان و حیوان نیز استفاده می شود. در بافتشناسی از آن برای سفید کردن ملانین استفاده میشود تا جزئیات بافت تیره رنگ ملانین آشکار شود. از پتاسیم پر منگنات می توان برای متفاوت کردن آمیلوئیدAA از دیگر آمیلوئیدها هم استفاده کرد. (آمیلوئیدها نوعی از پروتئینها هستند که در صورت تجمع بی جا باعث بیماری آمیلوئیدوز می شوند، برای اطلاعات بیشتر واژهٔ Amyloid را در ویکیپدیای انگلیسی ببینید) پتاسیم پرمنگنات باعث میشود که آمیلوئیدAA به وسیلهٔ رنگ سرخ کنگو (congo red) رنگ آمیزی نشود، این در حالی است که دیگر آمیلوئیدها به وسیلهٔ سرخ کنگو رنگ می شوند. در یک بازهٔ زمانی از پتاسیم پرمنگنات برای درمان سوزاک استفاده شد و همچنین از آن هنوز در درمان برفک استفاده می شود.
سنتزهای شیمی آلی
مهمترین و بزرگترین کاربردهای پتاسیم پرمنگنات، استفاده از آن به عنوان واکنشگر در سنتزبرخی مواد آلی بروش اکسایش است. مثلا ترکیباتی بنزوآلکیل به اسیدها اکسید می شوند.
تصفیه پسابهای صنعتی
بدلیل خاصیت اکسیدکنندگی قوی و قیمت ارزان، در تصفیه پسابهای صنعتی است.
عیار سنجی در شیمی تجزی
یکی از روشهای مرسوم در تعیین غلظت مواد در صنعت و هست. در عیارسنجیهای اکسایش - کاهش یکی از معرفهای پرکاربرد پرمنگنات است که بدلیل رنگ بنفش خود، نیاز به شناساگر هم ندارد. از این ترکیب برای عیارسنجی ترکیباتی آب اکسیژنه و استفاده میشود.
| این یک نوشتار خُرد پیرامون شیمی است. با گسترش آن به ویکیپدیا کمک کنید. |
فرمول شیمیایی
|
|
ممکن است این مقاله نیازمند ویکیسازی باشد تا با استانداردهای کیفی ویکیپدیا همخوانی یابد. خواهشمندیم با افزودن پیوندهای داخلی مرتبط، یا با بهبود چیدمان به بهبود آن کمک کنید. |
فرمول شیمیایی و یا فرمول مولکولی یک راه برای بیان اطلاعات مربوط به اتمهای تشکیل دهنده یک ترکیب شیمیایی خاص است. با تکیه بر فرمول تجربی به تنهایی، یک مولکول متان برای مثال ممکن است شامل یک کربن و چهار هیدروژن یا دو کربن و هشت هیدروژن با هر مضربی از CH۴ باشد. ما باید فرمول مولکولی یعنی:فرمولی که شمار واقعی هر نوع اتم را در یک مولکول نشان دهد را نیز باید پیدا کنیم.
برای پیدا کردن فرمول مولکولی باید وزن مولکولی را تعیین کنیم، امروزه وزن مولکولی را با طیف سنجی جرمی که به طور مطمئن مقدار دقیق آن را به دست میدهد اندازه میگیرند برای مثال اتان دارای فرمول تجربی CH۳ است برای آن وزن مولکولی ۳۰ به دست میآید که نشان میدهد از میان فرمولهای مولکولی ممکن فرمول صحیح باید C۲H۶ باشد.
منابع
- کتاب شیمی آلی ۱ نوشته تورنتون موریسون و نیلسون بوید مترجمان: دکتر علی سیدی اصفهانی، دکتر عیسی یاوری و دکتر احمد میرشکرائی صفحهٔ ۸۸
[نمایش]
ترکیبات سدیم
لگاریتم
لُگاریتم یک عدد در یک پایه، برابر با توانی از پایهاست که آن عدد را میدهد. برای نمونه لگاریتم ۱۰۰۰ در پایهٔ ۱۰، برابر با ۳ است. چون ۱۰ × ۱۰ × ۱۰ = ۱۰۰۰ یا به بیان کلیتر اگر x = by باشد آنگاه لگاریتم x در پایهٔ b برابر با y خواهد بود و به زبان ریاضی آن را به صورت  نمایش میدهیم. مانند:
نمایش میدهیم. مانند: 
لگاریتم نخستین بار از سوی جان نپر در اوایل سده ۱۷ میلادی به عنوان وسیلهای برای آسان تر کردن محاسبات، معرفی شد؛ که به سرعت از سوی دانشمندان و مهندسان پذیرفته شد و برای آسانتر کردن و سریعتر کردن محاسبه جدولهای لگاریتم اعشاری و ایجاد شدند و مورد استفاده قرار گرفتند. تمامی این ابزارها بر پایهٔ این مفهوم که «لگاریتم حاصل ضرب برابر است با مجموع لگاریتمها»، ساخته شده بودند:
مفهوم امروزی لگاریتم از تلاشهای لئونارد اویلر در قرن ۱۸ گرفته شده است؛ او توانست مفهوم لگاریتم را با مفهوم تابع نمایی پیوند دهد.
لگاریتم در پایهٔ ۱۰ را لگاریتم اعشاری مینامند که کاربرد بسیار زیادی در مهندسی دارد. لگاریتم در مبنای ثابت e یا عدد نپر ≈ ۲٫۷۱۸ را لگاریتم طبیعی مینامند. این لگاریتم در ریاضیات محض بویژه حساب دیفرانسیل و انتگرال بسیار کاربرد دارد. نیز در مبنای ۲ نوشته میشود و کاربرد زیادی در علوم رایانه دارد.
به کمک مقیاس لگاریتمی، میتوان اندازههای بسیار بزرگ را در ابعاد بسیار کوچکتری نشان داد برای نمونه دسیبل یکایی لگاریتمی است که برای نشان دادن و نسبت ولتاژ کاربرد دارد. در شیمی نیز پ هاش که معیاری برای نشان دان میزان اسیدی بودن مایعات است در مقیاس لگاریتمی بیان میشود. همچنین لگاریتم در نظریهٔ پیچیدگی محاسباتی و در برخی شکلهای هندسی مانند برخالها کاربرد دارد. از دیگر کاربردهای آن میتوان به فاصله در موسیقی و رابطههای شمارش اعداد اول اشاره کرد.
تابع توان وارون تابع لگاریتم است و لگاریتم مختلط، تابع وارون تابع نمایی به کار رفته در اعداد مختلط است. لگاریتم گسسته نیز در رمزنگاری کلید عمومی استفاده میشود.
محتویات |
انگیزهٔ اولیه و تعریف
انگیزهٔ ساخت لگاریتم، داشتن وارون تابع توان بودهاست. برای نمونه، توان سوم ۲، ۸ است چون ۸ = ۲ × ۲ × ۲ = ۲۳ پس لگاریتم ۸ در پایهٔ ۲، ۳ میشود.
به توان رساندن
توان سوم عددی مانند b برابر است با 3 بار ضرب b در خودش. حال اگر b به توان یک عدد طبیعی مانند n برسد به معنی n بار ضرب کردن b در خودش است که به صورت زیر نمایش میدهیم:
در صورتی که n عدد طبیعی نباشد، آنگاه bn جواب دیگری خواهد داشت. مانند 1- که b-1 برابر معکوس b است.[nb ۱]
تعریف
لگاریتم عددی مانند y در پایهٔ b عبارت است از یافتن عددی که اگر b به توان آن عدد برسد برابر با y شود. به عبارت دیگر جواب x معادلهٔ زیر برابر با لگاریتم y در پایهٔ b خواهد بود.[۲]
پایهٔ b باید یک عدد حقیقی y نیز باید یک عدد مثبت باشد.[۲]
چند نمونه
- نمونهٔ یکم
برای نمونه ۴ = (۱۶) log۲ چون ۱۶ = ۲ × ۲ × ۲ × ۲ = ۲۴
- نمونهٔ دوم
برای توانهای منفی نیز لگاریتم معتبر است مانند:
چون
- نمونهٔ سوم
(۱۵۰) log۱۰ تقریباً برابر است با ۲٫۱۷۶ عددی میان ۲ و ۳ چون ۱۵۰ خود عددی است میان ۱۰۰ = ۱۰۲ و ۱۰۰۰ = ۱۰۳ همچنین در هر پایهای  و
و  چون به ترتیب:
چون به ترتیب: 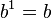 و
و  است.
است.
قوانین لگاریتم
رابطههای مختلفی به عنوان قوانین لگاریتم وجود دارند که میتوانند میان فرمولهای لگاریتمی رابطه برقرار کنند.
ضرب، تقسیم، توان، ریشه
لگاریتم حاصل ضرب چند عدد برابر است با مجموع لگاریتمهای تک تک آن عددها. لگاریتم نسبت دو عدد (تقسیم) برابر است با تفاضل لگاریتم آن دو عدد. لگاریتم توان p ام یک عدد برابر است با p برابر لگاریتم آن عدد. لگاریتم ریشهٔ p ام یک عدد برابر است با لگاریتم آن عدد تقسیم بر p. جدول زیر قوانین لگاریتم را همراه با یک نمونه نشان دادهاست:
| رابطه | نمونه | |
|---|---|---|
| ضرب |  |
 |
| تقسیم |  |
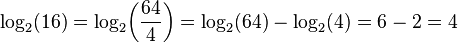 |
| توان | 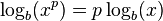 |
 |
| ریشه | ![log_b sqrt[p]{x} = frac {log_b (x)} p ,](http://upload.wikimedia.org/math/3/c/a/3ca49ea6d6cf9ced59d76f8fc5e42755.png) |
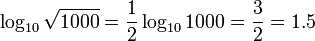 |
تغییر پایه
میتوان 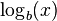 را به صورت غیر مستقیم با گرفتن لگاریتم x و b در یک پایهٔ دلخواه مانند k بدست آورد، به این ترتیب که:
را به صورت غیر مستقیم با گرفتن لگاریتم x و b در یک پایهٔ دلخواه مانند k بدست آورد، به این ترتیب که:
بیشتر ماشین حسابهایی که در دسترس اند لگاریتم را تنها در مبنای ۱۰ و عدد نپر[۳] محاسبه میکنند و لگاریتم در پایههای دیگر را به کمک رابطهٔ بالا محاسبه میکنند:
همچنین اگر عددی مانند x و مقدار لگاریتم آن را در یک مبنای نامشخص b داشته باشیم 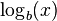 حال میتوان مبنای نامشخص b را به ترتیب زیر محاسبه کرد:
حال میتوان مبنای نامشخص b را به ترتیب زیر محاسبه کرد:
پایههای ویژه
پایههای ویژهٔ لگاریتم عبارتند از ۱۰، ۲ و عدد e (عدد گنگی تقریباً برابر با ۲٫۷۱۸۲۸) در آنالیز ریاضی لگاریتم در پایهٔ عدد e بسیار کاربرد دارد، لگاریتم در پایهٔ ۱۰ را میتوان بوسیلهٔ ماشین حسابهای دستی که در اختیار است به آسانی محاسبه کرد:[۴]
لگاریتم در پایهٔ ۱۰ را میتوان به آسانی با شمردن تعداد رقمهای یک عدد بدست آورد. برای نمونه (۱۴۳۰) log۱۰ تقریباً برابر است با ۳٫۱۵ چون ۱۴۳۰ چهار رقم دارد پس لگاریتم آن در پایهٔ ۱۰ باید عددی میان ۳ و ۴ باشد. لگاریتم در پایهٔ ۲ در علوم رایانه مورد استفاده قرار میگیرد چون در آن از دستگاه اعداد دودویی استفاده میشود.
جدولی که در ادامه قرار داده شدهاست علامتهایی که برای نشان دادن تابع لگاریتم کاربرد دارند و جایی که هر نوع لگاریتم مورد استفاده قرار میگیرد را نشان دادهاست. در بسیاری موارد اگر بتوان از روی نوشته تشخیص داد تنها از نماد لگاریتم استفاده میکنند و از نوشتن پایهٔ آن خودداری میکنند. در جدول زیر نمادی ستون «نماد ISO» مربوط به پیشنهادی است که از سوی سازمان بینالمللی استانداردسازی[۵] داده شدهاست.(ISO 31-11)
| پایهٔ b | نام گونهٔ لگاریتم | ISO نماد در | دیگر نمادها | کاربرد |
|---|---|---|---|---|
| ۲ | lb(x)[۶] | ld(x)، log(x) (در علوم رایانه)، lg(x) |
علوم رایانه، نظریهٔ اطلاعات | |
| e | لگاریتم طبیعی | ln(x)[nb ۲] | log(x) (در ریاضی و بسیاری از زبانهای برنامه نویسی[nb ۳]) |
آنالیز ریاضی، فیزیک، شیمی آمار, علم اقتصاد, و بعضی از زمینههای مهندسی |
| ۱۰ | لگاریتم اعشاری | lg(x) | log(x) (در مهندسی، زیست شناسی، اخترشناسی), |
در زمینههای گوناگون مهندسی (مانند دسیبل)، تهیه جدول لگاریتم و ماشین حسابهای مهندسی |
پیشینه
پیشینیان
از کسانی بود که با مفهومی به نام ardhaccheda کار کرد. ardhaccheda یعنی تعداد دفعاتی که میتوان ۲n را نصف کرد. برای نمونه برای توانهای دقیق ۲ این کار برابر با لگاریتم گرفتن در مبنای ۲ بود؛ وی همچنین لگاریتم در پایهٔ دیگر اعداد صحیح مانند لگاریتم در پایهٔ ۳ (trakacheda) و در پایهٔ ۴ (caturthacheda) را نیز معرفی کرد.[۱۰][۱۱] در سال ۱۵۴۴ میلادی در نورنبرگ Arithmetica integra را منتشر کرد، در این نوشته جدولی از اعداد صحیح و توانهای ۲ داده شده بود، این جدول به عنوان نسخهٔ اولیهٔ جدول لگاریتم شمرده میشود.[۱۲][۱۳]
از نپر تا اویلر

روش لگاریتمگیری در سال ۱۶۱۴ از سوی جان نپر در کتابی با عنوان Mirifici Logarithmorum Canonis Descriptio (توصیفی بر قانون شگفتانگیز لگاریتم) ارائه شد.[۱۴] همچنین (به فرانسوی: Joost Bürgi) نیز جداگانه روش لگاریتمگیری را پیدا کرده بود اما آن را شش سال پس از نپر منتشر کرد.[۱۵]
نپر، با استفاده از روش تقسیمهای متوالی توانسته بود عبارت  را به ازای Lهای میان ۱ تا ۱۰۰ محاسبه کند. جواب این عبارت برای ۱۰۰ = L تقریباً برابر است با ۰٫۹۹۹۹۹ = ۱ - ۵-۱۰ و ۲۰ ۰٫۹۹۵ ≈ ۰٫۹۹. این محاسبات که ۲۰ سال طول کشید، باعث شد تا او بتواند به ازای هر عدد N در بازهٔ ۵ تا ۱۰ میلیون، بتواند عدد L را پیدا کند که در رابطهٔ زیر صدق کند:
را به ازای Lهای میان ۱ تا ۱۰۰ محاسبه کند. جواب این عبارت برای ۱۰۰ = L تقریباً برابر است با ۰٫۹۹۹۹۹ = ۱ - ۵-۱۰ و ۲۰ ۰٫۹۹۵ ≈ ۰٫۹۹. این محاسبات که ۲۰ سال طول کشید، باعث شد تا او بتواند به ازای هر عدد N در بازهٔ ۵ تا ۱۰ میلیون، بتواند عدد L را پیدا کند که در رابطهٔ زیر صدق کند:
نپر ابتدا نام «عدد ساختگی» را بر L نهاد ولی پس از مدتی واژهٔ «لگاریتم» logarithm را معرفی کرد و آن را بر عددی گذاشت که نمایندهٔ یک نسبت است: واژهٔ λόγος برابر logos به معنی «نسبت» است و واژهٔ ἀριθμός برابر arithmos به معنی «عدد» است. بوسیلهٔ عبارت زیر میتوان مفهوم پیشین لگاریتم را با مفهوم امروزی لگاریتم طبیعی مرتبط کرد:[۱۶]
با تقریب خوبی داریم:
این دستآورد خیلی زود مورد تحسین گستردهٔ دیگران قرار گرفت، به همین دلیل با تلاش دانشمندانی چون (Bonaventura Cavalieri) از ایتالیا، (Edmund Wingate) از فرانسه، زو فنگزوئو (Xue Fengzuo) از چین و... مفهوم لگاریتم همه جا فراگیر شد.[۱۷]
در سال ۱۶۴۷ توانست مفهوم لگاریتم را با یک چهارم هذلولی مرتبط کند، با فرض آنکه سظح  زیر منحنی هذلولی به ازای ۱ = x تا t در رابطهٔ زیر صدق میکند:
زیر منحنی هذلولی به ازای ۱ = x تا t در رابطهٔ زیر صدق میکند:
لگاریتم طبیعی اولین بار از سوی در مقالهٔ Logarithmotechnia که در سال ۱۶۶۸ منتشر کرد، توضیح داده شد.[۱۸] البته پیش از او جان اسپیدل که یک معلم ریاضی بود در سال ۱۶۱۹ جدولی از لگاریتم طبیعی را گردآوری کرده بود.[۱۹] در حدود سال ۱۷۳۰ لئونارد اویلر تابع نمایی و لگاریتم طبیعی را به گونهٔ زیر تعریف کرد:
همچنین اویلر نشان داد که این دو تابع وارون یکدیگرند.[۲۰][۲۱][۲۲]
جدول لگاریتم، خطکش لغزان و کاربردها در گذشته

با ساده سازی محاسبات پیچیده، از لگاریتم میتوان در دانش پیشرفته مانند اخترشناسی، نقشه برداری، هوانوردی و ... کمک گرفت. پیر سیمون لاپلاس دربارهٔ لگاریتم گفتهاست:
وسیلهای ستودنی است که به کمک آن کار چند ماه به چند روز کاهش مییابد، عمر اخترشناسان را دو برابر میکند و از خطاهای کوچک میگذرد و از جملههای طولانی و جدانشدنی ریاضی بیزار است.
وسیلهٔ کلیدی که پیش از در دسترس قرار گرفتن ماشین حساب و رایانه برای محاسبهٔ لگاریتم از آن استفاده میشد و بوسیلهٔ آن بود که ارزش لگاریتم روشن شد، جدول لگاریتم بود.[۲۴] چنین جدولی برای اولین بار بوسیلهٔ در سال ۱۶۱۷ بلافاصله پس از ابتکار نپر ایجاد شد. پس از آن جدولهای وسیع تر و دقیق تری نوشته شد. در این جدولها مقدار 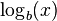 و
و 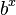 برای هر عدد x در یک بازهٔ مشخص با دقت مشخص و برای پایههای مشخص (معمولاً پایهٔ ۱۰) نوشته شده بود. برای نمونه در اولین جدول بریگز، لگاریتم طبیعی اعداد صحیح میان ۱ تا ۱۰۰۰ با دقت ۸ رقم اعشار نوشته شده بود. از آنجایی که تابع
برای هر عدد x در یک بازهٔ مشخص با دقت مشخص و برای پایههای مشخص (معمولاً پایهٔ ۱۰) نوشته شده بود. برای نمونه در اولین جدول بریگز، لگاریتم طبیعی اعداد صحیح میان ۱ تا ۱۰۰۰ با دقت ۸ رقم اعشار نوشته شده بود. از آنجایی که تابع 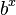 وارون
وارون
قضیه فیثاغورس
قضیهٔ فیثاغورس در هندسه و فضای اقلیدسی بخشی از صورت کلی قانون کسینوسها هنگامی که زاویهٔ بین دو بردار ۹۰ درجهاست میباشد. این قضیه به نام ریاضیدان یونانی فیثاغورس نامگذاری شدهاست. به سخن دیگر در یک مثلث راستگوشه (قائم الزاویه) همواره مجموع توانهای دوم دو ضلع برابر با توان دوم ضلع سوم است.
قانون کسینوسها بیان میکند که اگر دو بردار (یا خط) a و b در راس O تشکیل یک زاویه با نام A بدهند بردار مجموع از رابطهٔ  بدست میآید.
بدست میآید.
همانطور که میبینید هر گاه زاویه A برابر با ۹۰ درجه باشد مقدار  صفر شده و در نتیجه صورت قضیهٔ فیثاغورس بدست میآید:
صفر شده و در نتیجه صورت قضیهٔ فیثاغورس بدست میآید:

وارون این قضیه نیز درست است، به عبارت دیگر، اگر  باشد، مثلث قائمالزاویه است. اثبات عکس قضیه فیثاغورس را به اقلیدس نسبت دادهاند.[۱]
باشد، مثلث قائمالزاویه است. اثبات عکس قضیه فیثاغورس را به اقلیدس نسبت دادهاند.[۱]
محتویات |
نمایشهای دیگر
اگر c طول وتر مثلث راستگوشه باشد و a و b طول دو ضلع دیگر آن، قضیهٔ فیثاغورس را به شکل رابطهٔ زیر مینویسیم:
و اگر مقدار a و b معلوم باشد c را به این شکل بدست میآوریم:
و اگر c معلوم باشد و یکی از دو ضلع a یا b نامعلوم، آنها را اینگونه بدست میآوریم:
یا
همانگونه که در پیشگفتار بیان شد، قضیهٔ فیثاغورس بخشی از صورت کلی قانون کسینوسها است.
فرمولها و راهنمای ریاضی ششم ابتدایی
1-هرگاه چند نقطهی متمایز(جدا از هم)،بر روی یک خط راست باشند تعداد پاره خط ها از فرمول زیر به دست می آید.
2 ÷ (تعداد فاصله ها × تعداد نقطه ها ) = تعداد پاره خط ها
توجه : تعداد فاصلهها همیشه یکی کمتر از تعداد نقطهها است.
2-هرگاه چند نقطهی متمایز،بر روی خط راست باشند، تعداد نیم خطها از فرمول زیر،به دست می آید.
2 × تعداد نقطهها = تعداد نیم خطها
3-هرگاه چند نقطهی متمایز، برروی یک نیم خط باشند،تعداد نیم خطها مانند مثال زیر به دست میآید.
مثال: برروی یک نیم خط،هفت نقطهی متمایز وجود دارد چند نیم خط،در شکل وجود دارد؟
پس (8 = 1 + 7 ) نقطه داریم یعنی 8 نیم خط خواهیم داشت.
4- هرگاه چند نقطهی متمایز، برروی یک پاره خط باشند نیم خطی، درشکل وجود ندارد.
برش و قسمت:
وقتی می خواهیم یک قطعه یا جسمی رشته مانند را به قسمت های مساوی ویا نامساوی تقسیم کنیم همیشه تعداد قسمتها یکی بیشتر از تعداد برشها است.
مثال: یک آهنگر , میله ای به طول 12 متر را به چهار قسمت تقسیم کرد او برای این کار چند برش زده است؟
برش 3 = 1 – 4 (قسمت)
مجموع و اختلاف:
هرگاه مجموع دو عدد و اختلاف آن دو عدد را به ما بدهند و آن دو عدد را از ما بخواهند، از دو راه زیر به دست میآید.
1-اگر مجموع واختلاف را از هم کم کرده،بر2 تقسیم کنیم عدد کوچکتر به دست میآید.
2- اگر مجموع واختلاف را با هم جمع کرده،بر2 تقسیم کنیم عدد بزرگتربه دست میآید.
تعداد یک رقم در یک مجموعهی اعداد متوالی

در تاریخ درخشان ایران زمین مفاخر بسیار زیادی وجود دارد که در زمان های دور با تحقیقات گستره و زحمت بسیار دستاورد های ارزنده ای برای دنیا به جای گذاشته اند. کتاب قانون در طب ابوعلی سینا یکی از هزاران یادگار فاخر و میراث گرانبها برای نسل بشر تا به امروز بوده که امروزه در دانشگاه های بزرگ دنیا به عنوان مرجع مشکل گشای محققان امروزی نیز است. امروز برای شما کتاب قانون طب ابوعلی سینا را آماده کردیم.

سری انیمیشن و بازی های پاندای کونگ فو کار ( Kung Fu Panda ) یکی از مشهورترین و محبوب ترین محصولاتی است که تا کنون تولید و به بازار عرضه شده است. این بار از سایت ” بازی های رایگان ” نسخه ی دوم این بازی را به صورت جاوا و در ابعاد ۱۷۶×۲۲۰ , ۲۴۰× ۳۲۰, ۳۲۰× ۲۴۰, ۳۶۰×۶۴۰ پیکسل ( مخصوص موبایل ) آماده کرده ایم. بازی Kung Fu Panda 2 با حجم بسیار کمی که دارد می تواند شما را ساعت ها سرگرم کرده و به یاد انیمیشن پاندای کونگ فو کار بیندازد.
حجم فایل : ۳٫۵۶ مگابایت
دانلود با لینک مستقیم از سرور سایت
پسورد فایل : www.freegame.com
جستجوهای ورودی:
دانلود بازی پاندای کونگ فو کار+ بازی پاندای کونگ فوکار+ بازی پاندای کونگ فو کار 2+ دانلود بازی پاندای کونگ فو کار 2+ بازی پاندای کونگ فو کار+ دانلود بازی پاندای کونگ فوکار برای کامپیوتر+ دانلود بازی پاندای کونگ فوکار+ دانلود بازی پاندای کونگ فو کار 2 برای کامپیوتر+ بازی پاندای کنگفوکار+ دانلود بازی پاندای کونگفو کار+ دانلود بازی پاندای کونگ فو کار1+ دانلود بازی کامپیوتری پاندای کونگ فو کار+ دانلود بازی کم حجم پاندای کونگ فوکار برای کامپیوتر+ بازی پاندای کونگ فوکار2+ دانلود بازی پاندا کونگ فو کار+ بازی پاندای کونگ فوکار+ دانلود رایگان بازی پاندای کونگ فوکار2+ دانلود بازی پاندای کونگفوکار+ دانلود بازی کم حجم پاندای کونگ فو کار+ دانلود بازی پاندای کنگفوکار+